Pytorch机器学习经典算法——线性回归

原视频链接：3. 零基础入门PyTorch之线性回归【逐行代码讲解】原文章链接：【PyTorch修炼】零基础入门PyTorch之线性回归【逐行代码讲解】

线性回归其实就是

y=kx+b

但是需要注意的是，这里所有的未知量都是一个矩阵而不是一个数，k是权重，b是偏差

要求：

数据都是tensor类型如果有batch_size需要用dataloader去装这个数据
建立 model
完成训练过程 ->进行前向传播 ->利用loss反向传播 ->优化器进行优化
用matlplotlib进行数据可视化

程序示例

导入库

1
2
3

import torch
import torch.nn as nn
import  matplotlib.pyplot as plt

写出函数并画图

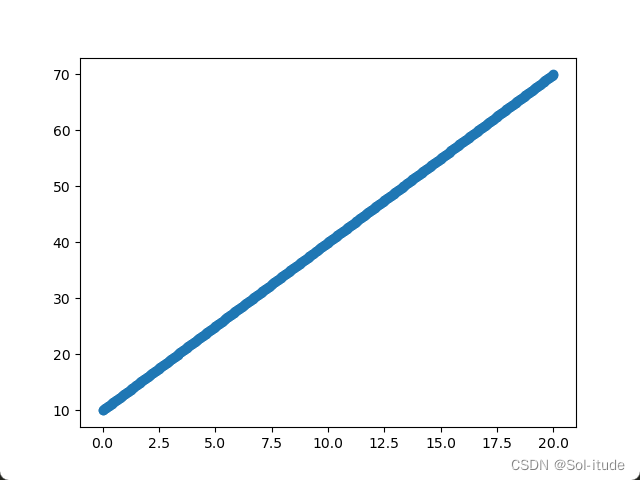
x=torch.linspace(0,20,500)#0-20之间取500个点
k=3
b=10
y=k*x+b

plt.scatter(x.data.numpy(),y.data.numpy())#因为torch的数据类型都是tensor，而plt只能画numpy数据结构的，所以需要写data.numpy()转换一下
plt.show()

输出结果： 在这里插入图片描述现在我们把写的函数都注释掉，来用机器学习拟合这条线

自己做一个数据集

x=torch.rand(512)#随机在0-1之间有512个点
noise=0.2*torch.randn(x.size())#加入高斯白噪声
k=3
b=10
y=k*x+b+noise
plt.scatter(x.data.numpy(),y.data.numpy())
plt.show()

输出结果： 在这里插入图片描述

构建神经网络

class LinearModel(nn.Module):
    def __init__(self,in_fea,out_fea):
        super(LinearModel, self).__init__()
        self.output=nn.Linear(in_features=in_fea,out_features=out_fea)
    def forward(self,x):
        x=self.output(x)
        return x
input_x=torch.unsqueeze(x,dim=1)#因为我们输入的x是512个数，而不是512，所以需要转换维度
input_y=torch.unsqueeze(y,dim=1)

构建损失函数和优化器

1
2
3

model=LinearModel()
loss_func=nn.MSELoss()#均方差求loss
optimizer=torch.optim.SGD(model.parameters(),lr=0.02)#随机梯度下降优化器

准备画图

1	plt.ion()#打开交互模型

开始训练

for step in range(20):
    pred=model(input_x)#预测值
    loss=loss_func(pred,input_y)#损失值
    optimizer.zero_grad()#梯度归零
    loss.backward()#反向传播
    optimizer.step()#进行优化器训练
    if step %10 ==0:#每十次移动一次
        plt.cla()#清除上一次的
        plt.scatter(input_x.data.numpy(),input_y.data.numpy())
        plt.plot(input_x.data.numpy(),pred.data.numpy(),'r-',lw=5)#画出预测的图像，线是红色，粗细是5
        [w,b]=model.parameters()
        plt.text(0,0.5,'loss=%.4f,k=%.2f,b=%.2f'%(loss.item(),k.item(),b.item()))
        plt.pause(1)#每次停顿一下

plt.ioff()#关闭实时显示
plt.show()

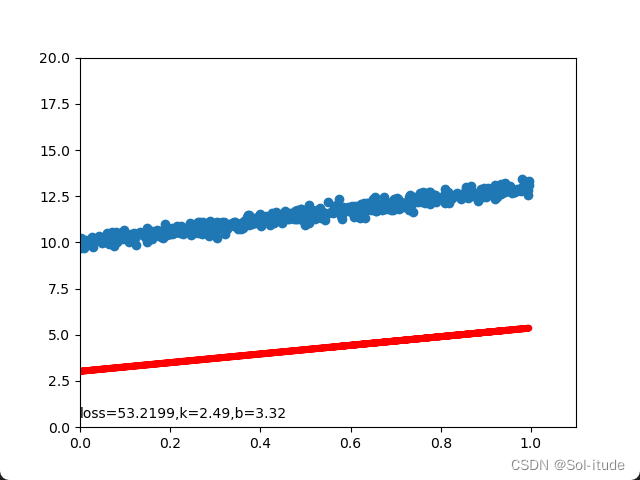
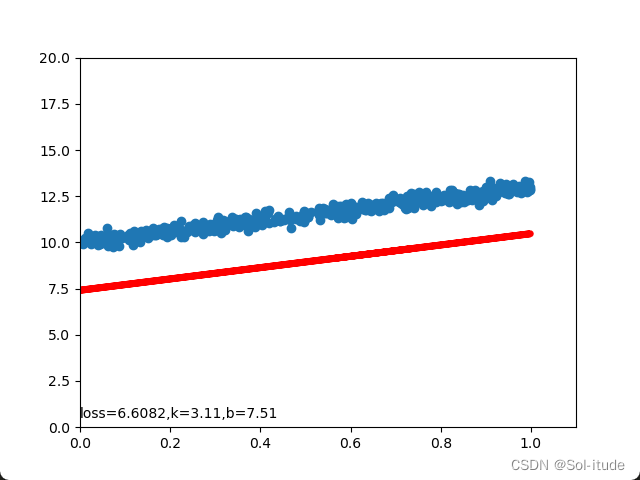
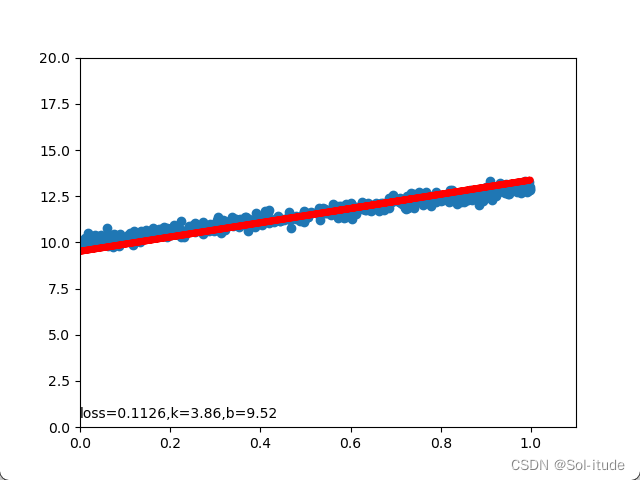
输出结果： 在这里插入图片描述可以看到红线正在逐渐拟合

完整代码

import torch
import torch.nn as nn
import  matplotlib.pyplot as plt

# x=torch.linspace(0,20,500)#0-20之间取500个点
# k=3
# b=10
# y=k*x+b
#
# plt.scatter(x.data.numpy(),y.data.numpy())#因为torch的数据类型都是tensor，而plt只能画numpy数据结构的，所以需要写data.numpy()转换一下
# plt.show()

x=torch.rand(512)#随机在0-1之间有512个点
noise=0.2*torch.randn(x.size())#加入高斯白噪声
k=3
b=10
y=k*x+b+noise
# plt.scatter(x.data.numpy(),y.data.numpy())
# plt.show()

class LinearModel(nn.Module):
    def __init__(self,in_fea,out_fea):
        super(LinearModel, self).__init__()
        self.output=nn.Linear(in_features=in_fea,out_features=out_fea)
    def forward(self,x):
        x=self.output(x)
        return x
input_x=torch.unsqueeze(x,dim=1)#因为我们输入的x是512个数，而不是512，所以需要转换维度
input_y=torch.unsqueeze(y,dim=1)

model=LinearModel(1,1)

loss_func=nn.MSELoss()#均方差求loss
optimizer=torch.optim.SGD(model.parameters(),lr=0.02)#随机梯度下降优化器


plt.ion()#打开交互模型
for step in range(200):
    pred=model(input_x)
    loss=loss_func(pred,input_y)
    optimizer.zero_grad()#梯度归零
    loss.backward()#反向传播
    optimizer.step()
    if step %10 ==0:
        plt.cla()
        plt.scatter(input_x.data.numpy(),input_y.data.numpy())
        plt.plot(input_x.data.numpy(),pred.data.numpy(),'r-',lw=5)#画出预测的图像，线是红色，粗细是5
        plt.xlim(0, 1.1)#防止x文本消失
        plt.ylim(0, 20)
        [w,b]=model.parameters()
        plt.text(0,0.5,'loss=%.4f,k=%.2f,b=%.2f'%(loss.item(),w.item(),b.item()))
        plt.pause(1)#每次停顿一下

plt.ioff()
plt.show()